过程:
实现模块:
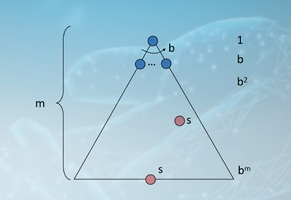
搜索树中的一些符号
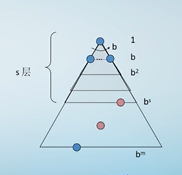
搜索树中的总节点个数:
1 + b + (b^2) + (b^3) + ... + (b^m) = (1 - b^(m + 1)) / (1 - b) = O(b^m)
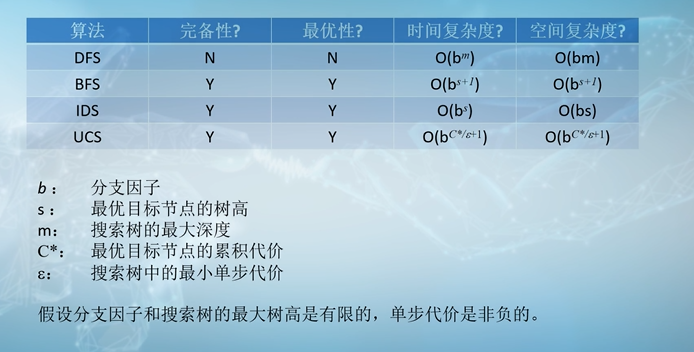
评价搜索算法的性质:
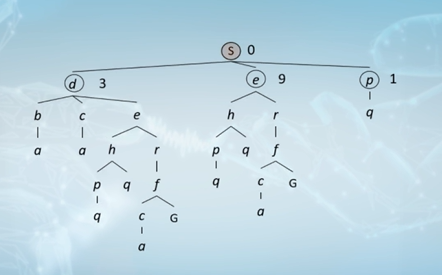
树搜索无法发现树中的重复结构,因此会产生额外的损耗。
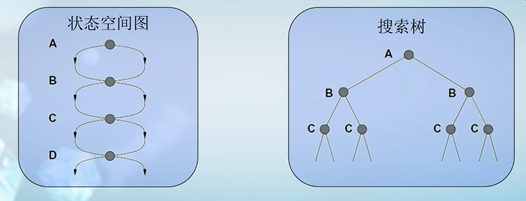
我们不需要扩展重复节点,因为,我们已经访问过该节点对应的状态了,而且代价更小。
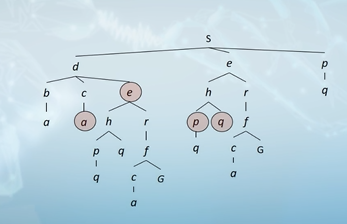
树搜索
// problem: 整个搜索问题
// fringe: 存储整个未搜索的节点
function TreeSearch(problem, fringe) return a solution, or failure {
//压入初始状态到未搜索的节点数据结构中
fringe = Insert(MakeNode(InitlalState[problem]), fringe)
// 循环的从该结构中压入或弹出节点进行操作
loop do{
//如果未访问的节点为空,还没有找到正确的节点,因此该问题没有解,则返回失败
if fringe is empty then return failure
//从fringe弹出一个节点
node = RemoveFront(fringe)
//该状态为想要的节点状态,则找到了,直接返回
if GoalTest(problem, STATE[node]) then return node
//扩展,生成和该节点相关的邻居节点,挨个遍历,然后将其插入到未访问的节点fringe数据结构中
for childNode in Expand(State[node], problem) {
fringe = Insert(childNode, fringe)
}
}
}
将上面的树搜索转换未图搜索, 引入一个closed数据结构,该结构未一个集合,用来保存已经访问过的节点,然后在加入到fringe中的时候查看下是否已经被访问过了,如果被访问过了,就不需要重复去访问了。
// problem: 整个搜索问题
// fringe: 存储整个已发现但是还未搜索访问过的节点
function GraphSearch(problem, fringe) return a solution, or failure {
closed = an empty set
//压入初始状态到未搜索的节点数据结构中
fringe = Insert(MakeNode(InitlalState[problem]), fringe)
// 循环的从该结构中压入或弹出节点进行操作
loop do{
//如果未访问的节点为空,还没有找到正确的节点,因此该问题没有解,则返回失败
if fringe is empty then return failure
//从fringe弹出一个节点
node = RemoveFront(fringe)
//该状态为想要的节点状态,则找到了,直接返回
if GoalTest(problem, STATE[node]) then return node
if STATE[node] is not in closed then
add STATE[node] to closed
//扩展,生成和该节点相关的邻居节点,挨个遍历,然后将其插入到未访问的节点fringe数据结构中
for childNode in Expand(State[node], problem) {
fringe = Insert(childNode, fringe)
}
}
}
在上面的算法框架中,从fringe中找一个节点来访问的策略不同,则有不同的搜索算法。选择边缘中深度最大的节点进行搜索(距离根节点步数量最多)为深度优先搜索DFS
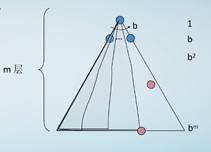
选择边缘中深度最小的节点进行扩展(距离根节点步数最少)为深度优先搜索DFS
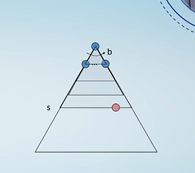
结合这两个的优点,可以得到一个算法,迭代加深算法,因为深度优先算法如果树很深就会一直往深度去搜,因此可以给其加一个深度限制,当搜索到限制的深度后在搜索其他的,就不要在继续往下了。
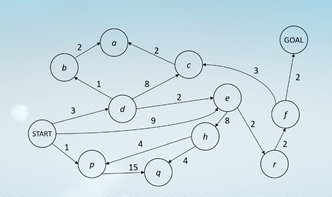
前面的算法默认每一步的代价都是一样的,但是大部分情况可能每一步的代价各不相同,比如如下: